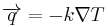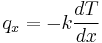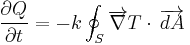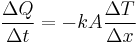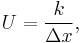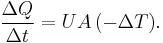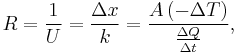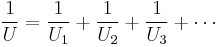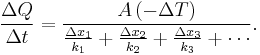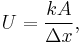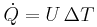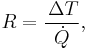Thermal conduction
In heat transfer, conduction (or heat conduction) is a mode of transfer of energy within and between bodies of matter, due to a temperature gradient. Conduction means collisional and diffusive transfer of kinetic energy of particles of ponderable matter (as distinct from photons). Conduction takes place in all forms of ponderable matter, viz. solids, liquids, gases and plasmas. Heat spontaneously tends to flow from a body at a higher temperature to a body at a lower temperature. In the absence of external driving fluxes, temperature differences, over time, approach thermal equilibrium.
In conduction, the heat flows through the body itself, as opposed to its transfer by the bulk motion of the matter as in convection, and by thermal radiation. In solids, it is due to the combination of vibrations of the molecules in a lattice or phonons with the energy transported by free electrons. In gases and liquids, conduction is due to the collisions and diffusion of the molecules during their random motion. Photons in general do not collide with one another and thermal transport by electromagnetic radiation is not regarded as conduction of heat. In solids, it is not simple to separate transfer by photons from transfer by ponderable matter, but the distinction can be more easily made in liquids, and is routinely made in gases.
In the engineering sciences, heat transfer includes the processes of thermal radiation, convection, and sometimes mass transfer and often more than one of these processes occurs in a given situation.
Contents |
Overview
On a microscopic scale, conduction occurs as rapidly moving or vibrating atoms and molecules interact with neighboring particles, transferring some of their kinetic energy. Heat is transferred by conduction when adjacent atoms vibrate against one another, or as electrons move from one atom to another. Conduction is the most significant means of heat transfer within a solid or between solid objects in thermal contact. Conduction is greater in solids because the network of relatively fixed spatial relationships between atoms helps to transfer energy between them by vibration.
Fluids (and especially gases) are less conductive. This is due to the large distance between atoms in a gas: fewer collisions between atoms means less conduction. Conductivity of gases increases with temperature. Conductivity increases with increasing pressure from vacuum up to a critical point that the density of the gas is such that molecules of the gas may be expected to collide with each other before they transfer heat from one surface to another. After this point conductivity increases only slightly with increasing pressure and density.
Thermal contact conductance is the study of heat conduction between solid bodies in contact. A temperature drop is often observed at the interface between the two surfaces in contact. This phenomenon is said to be a result of a thermal contact resistance existing between the contacting surfaces. Interfacial thermal resistance is a measure of an interface's resistance to thermal flow. This thermal resistance differs from contact resistance, as it exists even at atomically perfect interfaces. Understanding the thermal resistance at the interface between two materials is of primary significance in the study of its thermal properties. Interfaces often contribute significantly to the observed properties of the materials.
The inter-molecular transfer of energy could be primarily by elastic impact as in fluids or by free electron diffusion as in metals or phonon vibration as in insulators. In insulators the heat flux is carried almost entirely by phonon vibrations.
Metals (e.g. copper, platinum, gold,etc.) are usually good conductors of thermal energy. This is due to the way that metals are chemically bonded: metallic bonds (as opposed to covalent or ionic bonds) have free-moving electrons which are able to transfer thermal energy rapidly through the metal. The "electron fluid" of a conductive metallic solid conducts most of the heat flux through the solid. Phonon flux is still present, but carries less of the energy. Electrons also conduct electric current through conductive solids, and the thermal and electrical conductivities of most metals have about the same ratio. A good electrical conductor, such as copper, also conducts heat well. Thermoelectricity is caused by the interaction of heat flux and electrical current. Heat conduction within a solid is directly analogous to diffusion of particles within a fluid, in the situation where there are no fluid currents.
To quantify the ease with which a particular medium conducts, engineers employ the thermal conductivity, also known as the conductivity constant or conduction coefficient, k. In thermal conductivity k is defined as "the quantity of heat, Q, transmitted in time (t) through a thickness (L), in a direction normal to a surface of area (A), due to a temperature difference (ΔT) [...]." Thermal conductivity is a material property that is primarily dependent on the medium's phase, temperature, density, and molecular bonding. Thermal effusivity is a quantity derived from conductivity which is a measure of its ability to exchange thermal energy with its surroundings.
Steady-state conduction
Steady state conduction is the form of conduction that happens when the temperature difference(s) driving the conduction are constant, so that (after an equilibration time), the spatial distribution of temperatures (temperature field) in the conducting object does not change any further. Thus, all partial derivatives of temperature with respect to space may either be zero or have nonzero values, but all derivatives of temperature at any point with respect to time are uniformly zero. In steady state conduction, the amount of heat entering any region of an object is equal to amount of heat coming out (if this were not so, the temperature would be rising or falling, as thermal energy was tapped or trapped in a region).
For example, a bar may be cold at one end and hot at the other, but after a state of steady state conduction is reached, the spatial gradient of temperatures along the bar does not change any further, as time proceeds. Instead, the temperature at any given section of the rod remains constant, and this temperature varies linearly in space, along the direction of heat transfer.
In steady state conduction, all the laws of direct current electrical conduction can be applied to "heat currents". In such cases, it is possible to take "thermal resistances" as the analog to electrical resistances. In such cases, temperature plays the role of voltage, and heat transferred per unit time (heat power) is the analog of electrical current. Steady state systems can be modelled by networks of such thermal resistances in series and in parallel, in exact analogy to electrical networks of resistors. See purely resistive thermal circuits for an example of such a network.
Transient conduction
In general, during any period in which temperatures are changing in time at any place within an object, the mode of thermal energy flow is termed transient conduction. Another term is "non steady-state" conduction, referring to time-dependence of temperature fields in an object. Non-steady-state situations appear after an imposed change in temperature at a boundary of an object. They may also occur with temperature changes inside an object, as a result of a new source or sink of heat suddenly introduced within an object, causing temperatures near the source or sink to change in time.
When a new perturbation of temperature of this type happens, temperatures within the system will change in time toward a new equilibrium with the new conditions, provided that these do not change. After equilibrium, heat flow into the system will once again equal the heat flow out, and temperatures at each point inside the system no longer change. Once this happens, transient conduction is ended, although steady-state conduction may continue if there continues to be heat flow.
If changes in external temperatures or internal heat generation changes are too rapid for equilibrium of temperatures in space to take place, then the system never reaches a state of unchaging temperature distribution in time, and the system remains in a transient state.
An example of a new source of heat "turning on" within an object which causes transient conduction, is an engine starting in an automobile. In this case the transient thermal conduction phase for the entire machine would be over, and the steady state phase would appear, as soon as the engine had reached steady-state operating temperature. In this state of steady-state equilibrium, temperatures would vary greatly from the engine cylinders to other parts of the automobile, but at no point in space within the automobile would temperature be increasing or decreasing. After establishment of this state, the transient conduction phase of heat transfer would be over.
New external conditions also cause this process: for example the copper bar in the example steady-state conduction would experience transient conduction as soon as one end was subjected to a different temperature from the other. Over time, the field of temperatures inside the bar would reach a new steady-state, in which a constant temperature gradient along the bar will finally be set up, and this gradient would then stay constant in space. Typically, such a new steady state gradient is approached exponentially with time after a new temperature-or-heat source or sink, has been introduced. When a "transient conduction" phase is over, heat flow may still continue at high power, so long as temperatures do not change.
An example of transient conduction which does not end with steady-state conduction, but rather no conduction, occurs when a hot copper ball is dropped into oil at a low temperature. Here the temperature field within the object begins to change as a function of time, as the heat is removed from the metal, and the interest lies in analyzing this spatial change of temperature within the object over time, until all gradients disappear entirely (the ball has reached the same temperature as the oil). Mathematically, this condition is also approached exponentially; in theory it takes infinite time, but in practice it is over, for all intents and purposes, in a much shorter period. At the end of this process with no heat sink but the internal parts of the ball (which are finite), there is no steady state heat conduction to be reached. Such a state never occurs in this situation, but rather the end of the process is when there is no heat conduction at all.
Analysis of non steady-state conduction systems is more complex than steady-state systems, and (except for simple shapes) calls for the application of approximation theories, and/or numerical analysis by computer. One popular graphical method involves the use of Heisler Charts.
Occasionally transient conduction problems may be considerably simplified if regions of the object being heated or cooled can be identified, in which thermal conductivity is very much greater than than that for heat paths leading into the region. In this case, the region with high conductivity can often be treated in the lumped capacitance model, as a "lump" of material with a simple thermal capacitance consisting of its aggregate heat capacity. Such regions show no temperature variation across their extent during warming or cooling (as compared to the rest of the system) due to their far higher conductance. During transient conduction, therefore, their temperature changes uniformly in space, and as a simple exponential in time. An example of such systems are those which follow "Newton's law of cooling" during transient cooling (or the reverse during heating). The equivalent thermal circuit consists of a simple capacitor in series with a resistor. In such cases, the remainder of the system with high thermal resistance (comparatively low conductivity) plays the role of the resistor in the circuit.
Relativistic conduction
The theory of relativistic heat conduction is a model that is compatible with the theory of special relativity. For most of the last century, it was recognized that Fourier equation is in contradiction with the theory of relativity because it admits an infinite speed of propagation of heat signals. For example, according to Fourier equation, a pulse of heat at the origin would be felt at infinity instantaneously. The speed of information propagation is faster than the speed of light in vacuum, which is physically inadmissible within the framework of relativity. Alterations to the Fourier model provided for a relativistic model of heat conduction, avoiding this problem.
Quantum conduction
Second sound is a quantum mechanical phenomenon in which heat transfer occurs by wave-like motion, rather than by the more usual mechanism of diffusion. Heat takes the place of pressure in normal sound waves. This leads to a very high thermal conductivity. It is known as "second sound" because the wave motion of heat is similar to the propagation of sound in air.
Fourier's law
The law of heat conduction, also known as Fourier's law, states that the time rate of heat transfer through a material is proportional to the negative gradient in the temperature and to the area, at right angles to that gradient, through which the heat is flowing. We can state this law in two equivalent forms: the integral form, in which we look at the amount of energy flowing into or out of a body as a whole, and the differential form, in which we look at the flow rates or fluxes of energy locally.
Newton's law of cooling is a discrete analog of Fourier's law, while Ohm's law is the electrical analogue of Fourier's law.
Differential form
The differential form of Fourier's Law of thermal conduction shows that the local heat flux density, 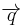 , is equal to the product of thermal conductivity,
, is equal to the product of thermal conductivity,  , and the negative local temperature gradient,
, and the negative local temperature gradient, 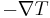 . The heat flux density is the amount of energy that flows through a unit area per unit time.
. The heat flux density is the amount of energy that flows through a unit area per unit time.
where (including the SI units)
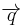 is the local heat flux, W·m−2
is the local heat flux, W·m−2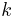 is the material's conductivity, W·m−1·K−1,
is the material's conductivity, W·m−1·K−1,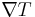 is the temperature gradient, K·m−1.
is the temperature gradient, K·m−1.
The thermal conductivity,  , is often treated as a constant, though this is not always true. While the thermal conductivity of a material generally varies with temperature, the variation can be small over a significant range of temperatures for some common materials. In anisotropic materials, the thermal conductivity typically varies with orientation; in this case
, is often treated as a constant, though this is not always true. While the thermal conductivity of a material generally varies with temperature, the variation can be small over a significant range of temperatures for some common materials. In anisotropic materials, the thermal conductivity typically varies with orientation; in this case  is represented by a second-order tensor. In nonuniform materials,
is represented by a second-order tensor. In nonuniform materials,  varies with spatial location.
varies with spatial location.
For many simple applications, Fourier's law is used in its one-dimensional form. In the x-direction,
Integral form
By integrating the differential form over the material's total surface  , we arrive at the integral form of Fourier's law:
, we arrive at the integral form of Fourier's law:
where (including the SI units)
: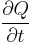 is the amount of heat transferred per unit time (in W) and is the amount of heat transferred per unit time (in W) and |
: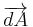 is an oriented surface area element (in m2) is an oriented surface area element (in m2) |
The above differential equation, when integrated for a homogeneous material of 1-D geometry between two endpoints at constant temperature, gives the heat flow rate as:
where
- A is the cross-sectional surface area,
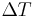 is the temperature difference between the ends,
is the temperature difference between the ends,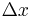 is the distance between the ends.
is the distance between the ends.
This law forms the basis for the derivation of the heat equation.
Conductance
Writing
where U is the conductance, in W/(m2 K).
Fourier's law can also be stated as:
The reciprocal of conductance is resistance, R, given by:
and it is resistance which is additive when several conducting layers lie between the hot and cool regions, because A and Q are the same for all layers. In a multilayer partition, the total conductance is related to the conductance of its layers by:
So, when dealing with a multilayer partition, the following formula is usually used:
When heat is being conducted from one fluid to another through a barrier, it is sometimes important to consider the conductance of the thin film of fluid which remains stationary next to the barrier. This thin film of fluid is difficult to quantify, its characteristics depending upon complex conditions of turbulence and viscosity, but when dealing with thin high-conductance barriers it can sometimes be quite significant.
Intensive-property representation
The previous conductance equations, written in terms of extensive properties, can be reformulated in terms of intensive properties.
Ideally, the formulae for conductance should produce a quantity with dimensions independent of distance, like Ohm's Law for electrical resistance: 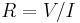 , and conductance:
, and conductance: 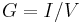 .
.
From the electrical formula: 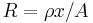 , where ρ is resistivity, x = length, and A is cross-sectional area, we have
, where ρ is resistivity, x = length, and A is cross-sectional area, we have 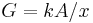 , where G is conductance, k is conductivity, x = length, and A = cross-sectional area.
, where G is conductance, k is conductivity, x = length, and A = cross-sectional area.
For Heat,
where U is the conductance.
Fourier's law can also be stated as:
analogous to Ohm's law: 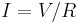 or
or 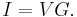
The reciprocal of conductance is resistance, R, given by:
analogous to Ohm's law: 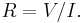
The rules for combining resistances and conductances (in series and in parallel) are the same for both heat flow and electric current.
Cylinders
Conduction through cylinders can be calculated when variables such as the internal radius 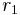 , the external radius
, the external radius 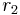 , and the length denoted as
, and the length denoted as 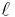 .
.
The temperature difference between the inner and outer wall can be expressed as 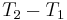 .
.
The area of the heat flow: 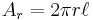
When Fourier’s equation is applied:
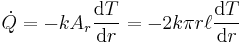
Rearranged:
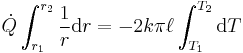
Therefore the rate of heat transfer is
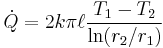
The thermal resistance is
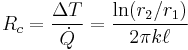
And 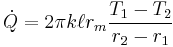 , where
, where 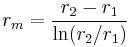 and it is important to note that this is the log-mean radius.
and it is important to note that this is the log-mean radius.
Spherical
internal radius 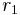 , the external radius
, the external radius 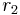 of a spherical shell, The surface area of a sphere is given by the following formula
of a spherical shell, The surface area of a sphere is given by the following formula
and solve rest of the spherical part as we solved for cylindrical shell(see above topic).
and finally we get
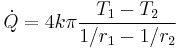
Zeroth law of thermodynamics
One statement of the so-called zeroth law of thermodynamics is directly focused on the idea of conduction of heat. Bailyn (1994) writes that "... the zeroth law may be stated:
-
- All diathermal walls are equivalent."[1]
A diathermal wall is a connection of contiguity between two bodies that allows the passage of heat by conduction between them.
This statement of the 'zeroth law' belongs to an idealized theoretical discourse, and actual physical walls do not match its grandiloquent generality.
But with suitable restrictions, the statement has physical import. For example, the material of the wall must not suffer a phase transition, such as evaporation or fusion, at the temperature at which it has to conduct heat. But when only thermal equilibrium is being considered, and time is not urgent, so that the conductivity of the material does not matter too much, one suitable conductor of heat is as good as another. Conversely, another aspect of the zeroth law is that, subject again to suitable restrictions, a given diathermal wall is indifferent to the nature of the heat bath to which it is connected. For example the glass bulb of a thermometer will act as a diathermal wall whether exposed to a gas or to a liquid, provided they do not corrode it or melt it.
These indifferences are amongst the defining characteristics of heat transfer. In a sense they are symmetries of heat transfer.
See also
- List of thermal conductivities
- Electrical conduction
- Convection diffusion equation
- U-value (insulation)
- Heat pipe
- Fick's law of diffusion
- Relativistic heat conduction
- Thermomass theory
- Churchill-Bernstein Equation
- Fourier number
- Biot number
References
- ^ Bailyn, M. (1994). A Survey of Thermodynamics, American Institute of Physics, New York, ISBN 0-88318-797-3, page 23.
- Dehghani, F 2007, CHNG2801 – Conservation and Transport Processes: Course Notes, University of Sydney, Sydney
- John H Lienhard IV and John H Lienhard V, 'A Heat Transfer Textbook', Third Edition, Phlogyston Press, Cambridge Massachusetts [1]
External links
- Heat conduction - Thermal-FluidsPedia
- Newton's Law of Cooling by Jeff Bryant based on a program by Stephen Wolfram, Wolfram Demonstrations Project.
- When Will My Turkey Be Done? is an example of applied heat conduction equations similar to Newton's Law of Cooling which predict the cooking time of turkeys and other roasts.